
Review |
 |
|
Web Resources
|
||
|
||
|
||
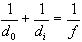
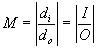
n = c / v n = lvac / lmed n1 sin q1 = n2 sin q2 vw = fl
| Converging Lenses | Diverging Lenses | |||||||||||||||||||||||||
| shape | "caved in" | "bowed out" | ||||||||||||||||||||||||
position of principal focus |
F is "behind the lens" on the opposite side of the lens as the incoming light |
F is "in front of the
lens" on the same side of the lens as the incoming light |
||||||||||||||||||||||||
| image position |
1/do + 1/di = 1/f do is always positive di is positive if real di is negative if virtual f is positive (convex) |
1/do + 1/di = 1/f do is always positive di is always negative (virtual) f is negative (concave) |
||||||||||||||||||||||||
| image
properties |
varies with do six case ray diagrams
|
virtual, upright, M < 1 ray diagrams
|
||||||||||||||||||||||||
| magnification | M = | di / do | = | I / O | | M = | di / do | = | I / O | | ||||||||||||||||||||||||
| rays | #1 top of
the object, parallel to the axis, strikes the lens, refracts through F #2 top of the object, passes through the center of the lens unbent #3 top of the object, aims for F', strikes the lens, refracts parallel to the axis |
#1 top of
the object, parallel to the axis, strikes the lens, refracts through F
(dot in line to F) #2 top of the object, passes through the center of the lens unbent #3 top of the object, aims for F', strikes the lens, refracts parallel to the axis (dot back refracted ray) |
| Copyright © 1997-2025 Catharine H. Colwell All rights reserved. PhysicsLAB Mainland High School Daytona Beach, FL 32114 |