When two parallel plates are connected across a battery, the plates become charged
and an electric field is established between them.
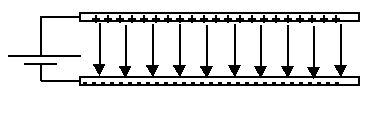
Remember that the direction of an electric field is defined as the direction that a
positive test charge would move. So in this case, the electric field would point
from the positive plate to the negative plate. Since the field lines are parallel to
each other, this type of electric field is uniform and is calculated with the equation E = V / d.
Note that the electric field strength, E, can be measured in either the
units V / m, or equivalently, N / C.
E = |
V / d |
|
(J / C) / m |
|
[ (nt m) / C] / m |
|
nt / C |
Since the field lines are parallel and the electric field
is uniform between two parallel plates, a test charge would experience the same force of
attraction or repulsion no matter where it was located. That force is
calculated with the equation F = qE.
In the diagram below, the distance between the plates is 0.14
meters and the voltage across the plates is 28V.
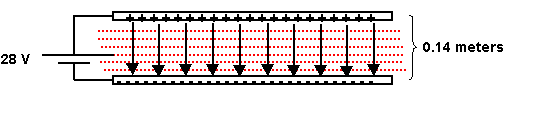
The UNIFORM electric field between the plates would be
| E = |
V / d |
|
28 / 0.14 |
|
200 V/m |
If a positive 2 nC charge were inserted anywhere between
the plates, it would experience a force of
| F = |
qE |
|
(2 x 10 – 9 ) (200) |
|
4.0 x 10 - 7 newtons |
in the direction of the negative,
bottom plate, no MATTER where it is placed in the region between the plates.
There are equipotential surfaces (surfaces where every point is at
the same voltage) between the plates which are equally spaced and parallel to the plates.
In the diagram shown, there are six surfaces, seven subregions, between the plates.
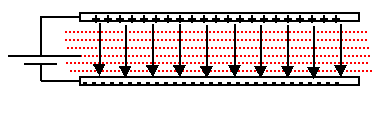
The distance from one surface to another would equal 0.14 / 7 or 0.02
meters. Therefore the potential difference from one equipotential surface to to the next
would equal
| DV = |
Ed |
|
(200)(0.02) |
|
4 volts |
The amount of work required to move a 2 nC charge from one equipotential
surface to another between the plates would equal
| W = |
q DV |
|
(2 x 10 – 9 ) (4) |
|
8.0 x 10 - 9 Joules |
This means, that a 2 nC charge would gain 8.0
x 10 - 9 Joules of EPE if moved towards the positive plate or it would gain 8.0
x 10 - 9 Joules of KE if released and it moved towards the negative plate.
No work is done when a charge is moved along an equipotential surface since all points on
the surface are at the same potential.
Capacitors
When two plates are charged and used in an electric
circuit, that configuration is called a capacitor. It's role in the
circuit is to store energy. Capacitors are rated in terms of capacitance which is
measured in farads. One farad equals the ratio of one coulomb per volt.
A parallel plate capacitor's effective capacitance is
defined in terms of its geometry.
C = eo A / d
where eo, the permittivity of free space, is a constant equal to
8.85 x 10 -12 F/m, A is the cross sectional
area of ONE plate, and d is the distance between the plates.
Dimensionally, this formula reduces to have a unit of farad.
Essentially, capacitance measures the relative amount
of charge that can be stored on a pair of parallel plate for a given amount of voltage.
If the capacitance increases, then more charge can be stored when the same
potential is applied.
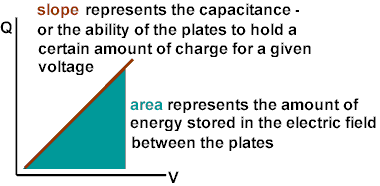
The equation for the line becomes Q = CV and the equation
for the area under the curve becomes E = ½ QV = ½ CV² .
The plates can then be discharged later through an external circuit. They are used when
the circuit requires a big burst of energy - like to "jump start" electric
motors, TV's or operate flash attachments on a camera.
Numerical Example #1
The gap in a certain
parallel-plate capacitor can be adjusted without otherwise disturbing the electric system.
In position A, the
capacitance is 4 x 10 -9 F and in
position B, the capacitance is 3.7 x 10 -9 F.
The capacitor is charged by a 12 volt battery when in position A.
The battery is then removed,
and the capacitor is moved to position B without changing the charge on it.
(A) How much charge is on the capacitor in position
A?
(B) What is the voltage across it in position B?
(C) By how much does its energy change as it goes
from position A to position B?
(D) What is the minimum amount of work that a person
holding the plates must have done to change the capacitor from A to B? |
The gap in a certain
parallel-plate capacitor can be adjusted without otherwise disturbing the electric system.
In position A, the
capacitance is 4 x 10 -9 F and in
position B, the capacitance is 3.7 x 10 -9 F.
The capacitor is charged by a 12 volt battery when in position A.
The battery remains attached to the
plates as the capacitor is moved to position B.
(A) How much charge is on the capacitor in position
A?
(B) What is the voltage across it in position
B?
(C) By how much does its energy change as it goes
from position A to position B?
(D) What is the minimum amount of work that a person
holding the plates must have done to change the capacitor from A to B? |
| Since the battery is removed during the transition
from position A to position B, the voltage is permitted to change
but the charge on the plates must
remain constant. |
Since the battery is NOT removed during the
transition from position A to position B, the voltage must remain
constant since it is regulated by the battery's presence in the circuit but the charge on the plates is permitted to change. |
(A) Q = CV ® Q = ( 4 x 10 -9 ) (12)
= 48 x 10 -9 C(B) VB = Q / C
® V = 48 x 10 -9 / 3.7 x 10 -9 =13 V
(C) E = ½ QV
® EA = ½ QV = ½ (48 x 10 -9)12
= 288 x 10 -9 J
® EB = ½ QV = ½ (48 x 10 -9)13
= 312 x 10 -9 J
(D) Work = DE = EB
- EA
Work = 312 x 10 -9
- 288 x 10 -9
= 24 x 10 -9 J |
(A) Q = CV
® QA = ( 4 x 10 -9 ) (12) = 48
x 10 -9 C
® QB = ( 3.7 x 10 -9 ) (12)
= 44.4 x 10 -9 C(B) VB
= 12 V
(C) E = ½ QV
® EA = ½ QV = ½ (48 x 10 -9)12
= 288 x 10 -9 J
® EB = ½ QV = ½ (44.4 x 10 -9)12
= 266 x 10 -9 J
(D) Work = DE = EB - EA
Work = 266 x 10 -9
- 288 x 10 -9
= - 22 x 10 -9 J |
If the electric field between the plates becomes too
strong, the air between them can no longer insulate the charges from sparking,
discharging, between the plates. In order to keep this from happening, a dielectric is
often inserted between the plates to reduce the strength of the electric field, without
having to reduce the voltage being placed across the plates. A dielectric is a polar
material whose electric field aligns to oppose the original electric field already
established between the plates. The dielectric is measured in terms of a
dimensionless constant, K, whose value is usually referenced from a table (K ³ 1). If this insulating material is
insufficient the capacitor can leak allowing current to flow between the plates. When this
occurs, the electric device "smells as if something is burning."
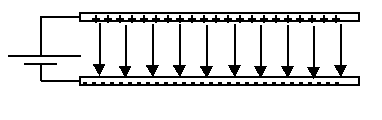
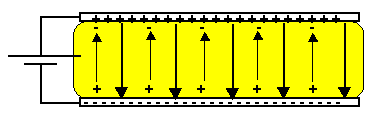 |
K = Eoriginal / Edielectric
K = Cdielectric / Coriginal
The dielectric
decreases the electric field strength between the plates while it increases their
capacitance. |
Numerical Example #2
| A parallel-plate air capacitor is charged by placing a
90-V battery across it. The battery is then removed, and an insulating, dielectric
fluid is inserted between the plates. The voltage across the capacitor is now 28-V. What is the dielectric constant of the fluid? |
A parallel-plate air capacitor holds a charge of
30 nC when a voltage of Vo is placed across its plates. When a dielectric
fluid is inserted between the plates, the charge on the plates increases to 87 nC if the
potential difference Vo is maintained.What is the
dielectric constant of the fluid? |
Since the battery is removed,
the voltage is permitted to change but the charge on the plates must remain constant.
The presence of the
dielectric also allows the capacitance of the
plates to be changed. |
Since the battery is NOT
removed, the voltage must remain constant since it is
regulated by the battery's presence in the circuit but the charge on
the plates is permitted to change.
The presence of the
dielectric also allows the capacitance of the
plates to be changed. |
Q = CV
® Qair
= Cair (90)
® Qdielectric
= Qair
® Cdielectric (28) = Cair
(90)K = Cdielectric / Cair
K = Cdielectric (28) = Cair (90)
K = Cdielectric
/ Cair = (90) / (28) = 3.2 |
Q = CV
® Qair = Cair (Vo) ® 30 x 10 -9 (Vo)
® Qdielectric = Cdielectric (Vo)
= 87 x 10 -9
(Vo)K = Cdielectric
/ Cair where C = Q / V
K = (Qdielectric / Vo) / (Qair / Vo )
K = [87 x 10 -9 (Vo) / Vo] / [30 x 10 -9 (Vo) / Vo ]
K = 87 x 10 -9 / 30 x 10 -9 = 2.9 |
Combinations
of Capacitors
When more than one capacitor is used in a circuit, the formula for a
collection of capacitors is
Qtotal = Ctotal x Vtotal
If the capacitors are arranged in series (one after another along a single path), then
Qtotal = Q1 = Q2 = Q3
Ctotal = (1/C1 + 1/C2 + 1/C3) -1
Vtotal = V1 + V2 + V3
If the capacitors arranged in parallel (strung along multiple paths that cross the same
section), then
Qtotal = Q1 + Q2 + Q3
Ctotal = C1 + C2 + C3
Vtotal = V1 = V2 = V3
Numerical Example #3
|

