| Newton's Three Laws |
|
Law of Inertia
Law of Acceleration
Law of Action-Reaction |
| centripetal force |
|
Fc = mac |
| centripetal acceleration |
|
ac = v ² / r |
| tangential velocity |
|
v = 2pr / T
v = rw where w = 2pf ( frequency in hz) |
| centripetal acceleration |
|
ac = 4p ² r / T ² |
relationship between
period (T) and frequency (f) |
|
f = 1 / T |
| centripetal acceleration |
|
ac = 4p ² r f ² |
| friction |
|
f = m N |
| conical pendulums |
|
T cos q = mg
T sin q = Fc = m v ² / r |
source of centripetal force
for a banked curve
when traveling at critical speed |
|
Fc = N sin q
[remember that N cos q = mg] |
| critical speed for a banked curve |
|
tan q = v ² / rg |
| universal gravitation |
|
F = G M 1 M 2 / r
² |
| universal gravitation constant |
|
6.67 x 10-11
N m ² / kg ² |
| Kepler's Third Law |
|
T ² / R ³ = 4p ² / G Mcentral
body
a unique constant for every satellite
system |
| gravitational field strength |
|
g = G Mcentral body / r ²
where r = Rcentral body + h |
| Kepler's Second Law |
|
vARA = vPRP
a satellite's tangential velocity and orbital radius
are inversely proportional |
|
|
|
critical velocity at the top of a
vertical circle
to achieve apparent weightlessness |
|
v = SQRT (rg) |
| apparent weight at the bottom of a
vertical circle |
|
N = mg + m v ² / r |
| Conservation of Energy |
|
S(PE
+ KE)before = S(PE
+ KE)after
PE = mgh
KE = ½ mv ² |
| height of a pendulum |
|
h = L - L cos q |
| kinematics equations |
|
s = vo t + ½ a t ²
vf ² = vo² + 2as
vf = vo + at
s = ½ ( vo + vf ) t |
| range of a projectile |
|
R = vH t |
| period of a pendulum |
|
T = 2p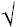 (
L / g ) (
L / g ) |
| tension in pendulum at angle a |
|
take components of weight
T - mg cos a = m v ² / r
mg sin a = matangential |

