Chapter

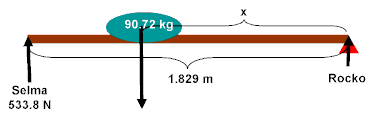
The board must first be placed in translational equilibrium; that is,
(A)  SF_x = 0 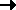SF_right =  SF_left

this requirement is not applicable since there are no horizontal forces

(B)  SF_y = 0 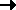SF_up =  SF_down

(beam is massless) S + R = (90.72)(9.8)
                        533.8 + R = 889

The board must then be placed in rotational equilibrium; that is,
 St = 0 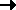St_cw =  St_ccw

pivot at Rocko: (533.8)(1.829) = (90.72)(9.8)(x)

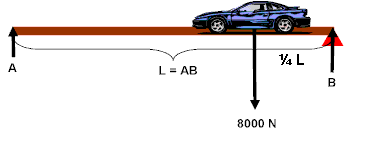
#33

For translational equilibrium:
(A)  SF_x = 0 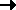SF_right =  SF_left

this requirement is not applicable since there are no horizontal forces

(B)  SF_y = 0 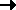SF_up =  SF_down

(bridge is massless) A + B = 8000

For rotational equilibrium:
 St = 0 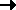St_cw =  St_ccw

pivot at B: A(L) = (8000)(¼L)

#37

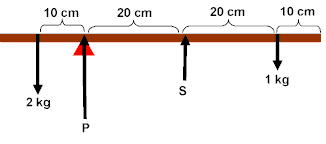
For translational equilibrium:
(A)  SF_x = 0 SF_right =  SF_left

this requirement is not applicable since there are no horizontal forces

(B)  SF_y = 0 SF_up =  SF_down

(beam is massless) S + P = 2(9.8) + 1(9.8)

For rotational equilibrium:
 St = 0 St_cw =  St_ccw

pivot at P: 1(9.8)(0.4) = 2(9.8)(0.1) + (S)(0.2)

#39 (see book for diagram)

For translational equilibrium:
(A)  SF_x = 0 SF_right =  SF_left

this requirement is not applicable since there are no horizontal forces

(B)  SF_y = 0 SF_up =  SF_down

top board: B + D = 480
bottom board: A + C = B

For rotational equilibrium:
 St = 0 St_cw =  St_ccw

top board - pivot at B: 480(9) = D(12)
bottom board - pivot at A: B(8) = C(12)

#60

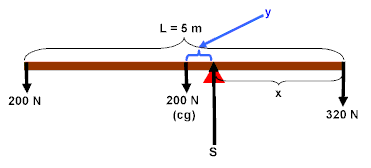
For translational equilibrium:
(A)  SF_x = 0 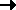SF_right =  SF_left

this requirement is not applicable since there are no horizontal forces

(B)  SF_y = 0 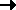SF_up =  SF_down

F_up = S = 200 + 320 + 200

For rotational equilibrium:
 St = 0 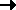St_cw=  St_ccw

pivot at S: 320(x) = 200(2.5+y) + 200(y)
note: uniform boards have their center of gravity in the middle
therefore  x + y = 2.5