AP Physics B: Capacitors
When two plates are charged and used in an electric circuit, that configuration is called a capacitor. It's role in the circuit is to store energy. Capacitors are rated in terms of capacitance which is measured in farads. One farad equals the ratio of one coulomb per volt.
A parallel plate capacitor's effective capacitance is
defined in terms of its geometry.
C = eo A / d
where eo, the permittivity of free space, is a constant equal to 8.85 x 10 -12 F/m, A is the cross sectional area of ONE plate, and d is the distance between the plates.
Dimensionally, this formula reduces to have a unit of farad: [C] = (F / m) (m² / m) = (F / m) (m) = F

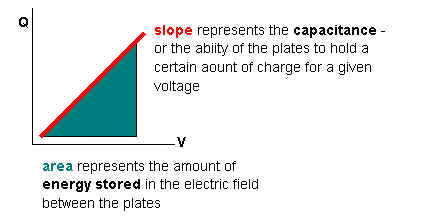
The equation for the line becomes Q = CV and the
equation for the area under the curve becomes
E = ½ QV = ½ CV² .
Capacitors are used in DC circuits to provide "bursts of energy." Typical examples would be a capacitor to jump start a motor or a capacitor used to operate a camera's flash.
When capacitors are used in DC circuits, transient currents will flow through any branch of the circuit where a capacitor is located until the capacitor is fully charged. then no currents will flow through that branch. Later, when a switch is closed, the capacitor can be discharged, at which time another transient current will flow until the capacitor no longer has any voltage.
Charged capacitors have voltage but not resistance: V = IR is not applicable since no currents flow THROUGH a capacitor. When a "loop" passes through a capacitor, it is treated like a "battery." That is, if the loop approaches the capacitor from "positive to negative" or "high to low" then the potential difference across the capacitor is written as -VC. Similarly, if the loop approaches the capacitor from "negative to positive" or "low to high" then the potential difference across the capacitor is written as +VC. Any resistors on the same branch of a circuit as a capacitor receive no current, and therefore do NOT lose any voltage.
Rules for capacitors arranged in series and parallel:
| charge | voltage | capacitance | |
| series | Qeq = Q1 = Q2 = Q3 | Veq = V1 + V2 + V3 | Ceq = ( C1-1 + C2-1 + C3-1) -1 |
| parallel | Qeq = Q1 + Q2 + Q3 | Veq = V1 = V2 = V3 | Ceq = C1 + C2 + C3 |