Thin lenses - devices
which refract light
converging lenses in air (chart)
thicker in the center than on the edges, convex
converge light - principal focus is to the right
usually form real inverted images (review 6 cases)
(#6) form enlarged virtual upright images when do < f
(#5) do not form any image when do = f (parallel rays)
(#4) form real enlarged images when 2f < do < f
(#3) form real images that are the same size as the object when do = 2f
(#2) form real reduced images when do > 2f
(#1) form point images when do Þ ¥
diverging lenses in air (chart)
thicker on the edges than in the center, concave
diverge light - principal focus is to the left
always form reduced virtual upright images

thin lens equation
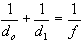
d o is always positive with a single lens
di is positive for real images,
negative for virtual images
f is positive for converging lenses, negative for diverging lenses
magnification
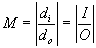
thin lenses in close combination
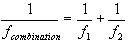
power of a lens
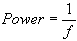
measured in Diopters
focal length must be measured in meters
Lens-maker's equation
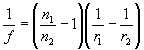
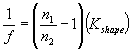
n 1 is the index of the lens
n2 is the index of the surrounding
medium
r1 is the radius of curvature for the
front surface (+ if convex, - if concave)
r2 is the radius of curvature for the
back surface (+ if convex, - if concave)
Kshape represents the shape of the
lens which does not change when placed in different mediums
double-lens systems
when drawing ray diagrams or using the thin-lens equation, work each lens separately
remember that the image of lens #1 is the object for lens #2
to calculate do for lens #2, subtract
di for lens #1 from the total
distance separating the lenses
the magnifications of the system is the product of the magnifications of each separate
lens
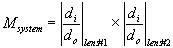
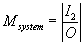
converging/converging and
converging/diverging systems
converging/converging can form a final image that is either real and upright or virtual
and inverted
converging/diverging form virtual inverted images
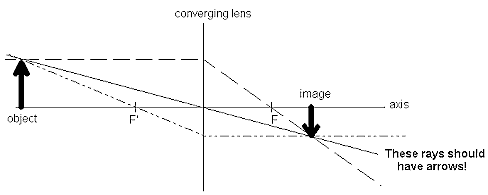
ray diagram for microscope - virtual image formed by eyepiece
Refraction
index of refraction
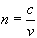
c = 3 x 108 m/sec
n > 1
the index is a measure of a medium's optical density (photon interaction with
electrons)
dispersion: a medium's index of refraction is actually frequency dependent
(spectrum)
Snell's Law
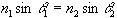
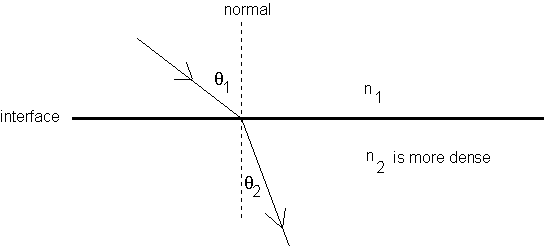
light bends towards the normal when it enters a more dense medium
light slows down when its travels through a more dense medium
the wavelength of light decreases as it travels through a more optically dense medium
the frequency of light is an invariant - it never changes
|

